乱谈partition算法

partition算法是一种分类算法，简单来说就把一个序列分成前后两部分，前一部分都是满足某一条件的元素，后一部分都是不满足该条件的元素。关于partition算法最著名的应用就是quick sort（快速排序）了。

除了快速排序外，partition算法还经常用在下列场合：

• 在O(N)的时间内找出一个序列中第k大（小）的元素。
• 在O(N)的时间内找出一个序列中所有比k大（小）的元素。

但是这一类场景使用的partition算法和快速排序使用的partition算法有一些略微的差别，如果不小心错用的话，就会产生意料之外的错误了。

快速排序的partition算法

简单来说就是通过partition算法将待排序序列划分为以pivot（中间）值为分界点的两个子序列，一个子序列所有元素的值都小于pivot，另一个子序列所有元素的值都大于等于pivot，然后再对每个子序列递归进行这样的操作。

常见的时间复杂度为Nlog(N)的排序算法有快速排序、堆排序、归并排序。一般来说在有大量的待排序序列数据的时候，快速排序是三种算法中表现最好的。

相较于堆排序，快速排序有更好的缓存局部性。在待排序数据量很大时，堆排序每次从二叉堆取出最大值，再放入一个较小的值，然后二叉堆调整其中各个元素时，从整个序列来看数据地址跨越的范围较大，发生cache未命中的几率增加，导致数据局部性变差。而快速排序，由于每次进行partition的时候数据交换都集中在当前的这一小段序列中，因此数据的地址跨越范围小，cache未命中的几率较小，数据局部性就更好了。

而对于归并排序，由于归并排序的空间复杂度是O(N)，每一层归并的时候都会发生数据从原始空间到辅助空间的拷贝或者从辅助空间到原始空间的拷贝，而原始空间是调用者申请的，辅助空间是被调用者自己申请的，所以从进程的虚拟地址空间上来讲两段空间的地址一般相差较大，这样每次拷贝的时候出现cache未命中的次数会升高，所以堆排序的局部性也不如快速排序。

下面这个动态图就是快速排序的基本过程：

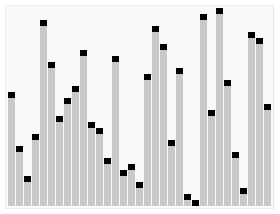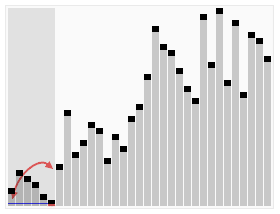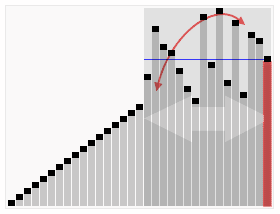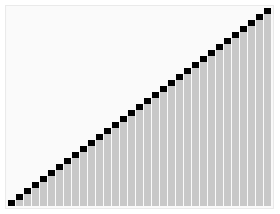
其中起关键作用的就是partition算法了:

int* partition(int* first, int* last, int pivot)
{
    while (true)
    {
        while (*first < pivot)
        {
            ++first;
        }
        --last;
        while (*last > pivot)
        {
            --last;
        }
        if (first >= last)
        {
            break;
        }
        swap(first, last);
        ++first;
    }
    return first;
}

以pivot为中间值将原序列划分为两个子序列，返回的指针指向第二个序列的首部。当然了，上面这种写法没有做指针的边界检查，也就代表了pivot值必须介于原序列最大值和最小值之间了（即min <= pivot <= max），否则就会产生越界。

下面是两个直观的过程示意图：

示例一

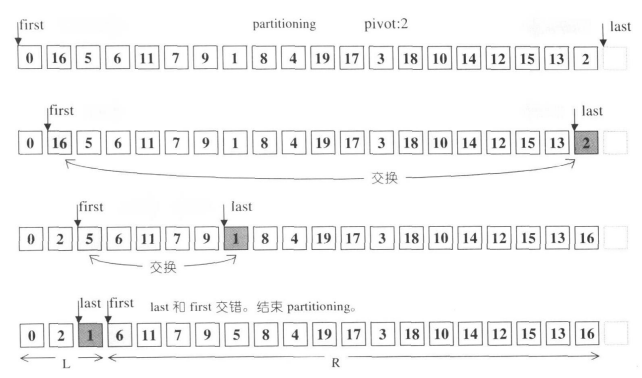
示例二

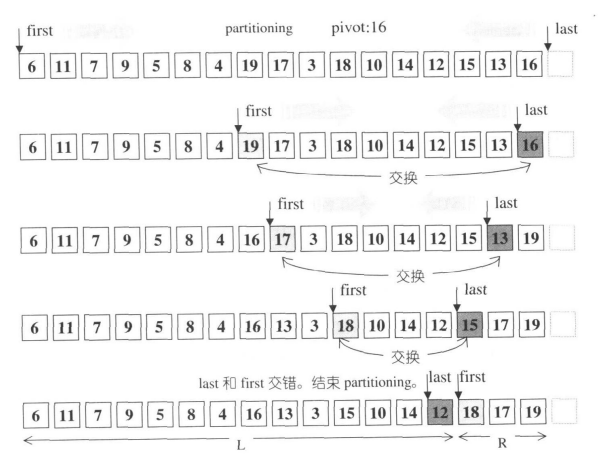
不知大家是否注意到在上面这种写法中，原序列里值等于pivot的元素经过partition后，可能出现在左边子序列中的任意位置，而不是两个子序列的中间位置。

适用其他场合的partition算法

我们知道还可以用partition算法来解决诸如「找出序列中第k小的元素」这一类问题，但是仔细推敲一下就会发现上文中适用于快速排序的partition算法不能用于这类情况了。

上一节最后提到了经过partition划分后，原序列中值为pivot的元素总是出现在左边的子序列中，而不是出现在两个子序列中间的位置，所以这就决定了它不适用于解决寻找序列第k小这一类问题。

例如对于寻找某一序列第k小元素中一场景，基本思路上这样的：

• 在序列中任取某一元素m，利用partition算法将原序列中所有小于m的元素移动至m的前面，把所有大于m的元素移动到m的后面。
• 经过partition划分后，若m的下标等于k，则m就是原序列中第k小的元素。若m的下标小于k，则代表第k小的元素在后面的子序列中，递归操作后面的子序列。若m的下标大于k，则代表第k小的元素在前面的子序列，递归操作前面的子序列。

其中关键点在于经过partition划分后，原序列中值为pivot的元素必须出现在划分的两个子序列的中间。而上文中的partition划分后，值为pivot的元素可能出现在左边子序列中的任意位置，但不是两子序列的中间。

下面是经过略微改动的partition，以适用于「寻找某序列第k小元素」这一类问题。

int* partition(int* first, int* last)
{
    if (first == NULL || last == NULL || first >= last - 1)
    {
        return first;
    }
    int* p = middle(first, last - 1, first + (last - first) / 2);
    int pivot = *p;
    *p = *--last;
    while (first < last)
    {
        while (first < last && *first <= pivot)
        {
            ++first;
        }
        *last = *first;
        while (first < last && *last >= pivot)
        {
            --last;
        }
        *first = *last;
    }
    *first = pivot;
    return first;
}

middle的作用是三值取中，最后返回的即是指向pivot的指针。

总结

• 对于快速排序，两种partition算法都适用。
• 对于寻找序列中第k小元素的一类问题，只有第二种partition算法适用，第一种不适用。