红黑树插入和删除的情况分析
红黑树是特殊二叉查找树的一种,一棵红黑树有以下5种性质:
- 根节点为黑色。
- 每个节点不是黑色就是红色。
- 每个红色节点的两个儿子一定是黑色。
- 所有的叶子节点都是黑色。(注:这里的叶子节点并不是真正意义上的叶子节点,而是一种只有颜色属性但不存放数据的节点,而且其没有儿子节点)
- 一个红黑树的中任取一个节点,从它所在位置到其他任何叶子节点的简单路径上所经过的黑色节点数相同。
这5个性质决定了从根节点到叶子节点的最长路径不可能大于最短路径的2倍。所以红黑树是一个大致平衡的二叉树。跟avl树不同,红黑树并不是严格平衡的,而avl树却是严格平衡的。
1. 插入
首先约定插入的新节点的颜色都为红色。然后将该节点插入的按二叉查找树的规则插入到树中。这个节点后文称为n
1. 根节点为空。这种情况,将n的颜色改为黑色即可。
2. n的父节点为黑色。这种情况不需要做修改。
3. n的父节点为红色(根据性质3,n的祖父节点必为黑色)。
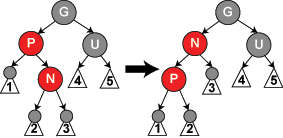
n的叔父节点为红色。这种情况,将n的父节点和叔父节点的颜色都改为黑色,若祖父节点是跟节点就将其改为黑色,否则将其颜色改为红色,并以祖父节点为插入的目标节点从情况1开始递归检测。
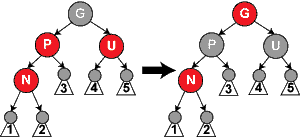
n的叔父节点为黑色, 且n和n的父节点在同一边(即父节点为祖父的左儿子时,n也是父节点的左儿子。父节点为祖父节点的右儿子时。n也是父节点的右儿子)。以父节点为祖父节的左儿子为例,将父节点改为黑色,祖父节点改为红色,然后以祖父节点为基准右旋。(n为父节点右儿子时做相应的左旋。)
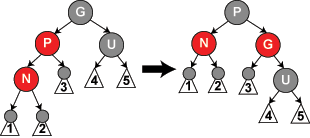
n的叔父节点为黑色,切n和n的父节点不在同一边(即父节点为祖父的左儿子时,n是父节点的右儿子。父节点为祖父节点的右儿子时。n也是父节点左右儿子)。以父节点为祖父节点的左儿子为例。以父节点为基准,进行左旋,然后以父节点为目标插入节点进入情况3的b情况进行操作。